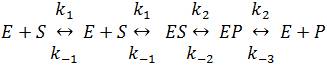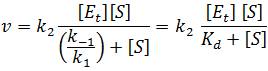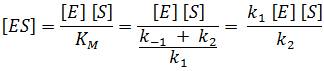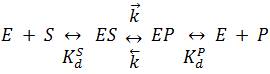Úvod

Experimentálně zjištěná závislost rychlosti v na koncentraci substrátu [S] obecné reakce katalyzované enzymem E podle následující rovnice (i) (Haldanův model)

velmi často vyhovuje následujícímu vztahu (ii)

,

kde [S] je koncentrace substrátu S, [E_t] je celková koncentrace enzymu E, V_max = k_kat . [Et] je maximální rychlost reakce, k_kat je rychlostní konstanta a K_M je Michaelisova konstanta. Komplexy ES a EP spolu s náležitými kinetickými konstantami modelu (i) v tomto případě považujeme za totožné. Závorky [ ] v textu a v rovnicích vždy označují látkovou koncentraci (mol . l^-1).

Mechanismus Michaelise-Mentenové

Jestliže je v modelu (i) ES ≡ EP, tj. meziprodukt EP se netvoří, ES se přímo rozpadá na E + P, k_-2 ≡ k_-3 zanedbáváme (reakci rozpadu ES považujeme za nevratnou; a k₂ ≡ k₃ ≪ k_-1, je [ES] v rovnováze s [E] a [S] a k2 určuje nejpomalejší stupeň v přímé reakci. Jde o mechanismus, který rozebrali L. Michaelis a M. L. Mentenová (1913).

Pro tuto reakci je

v = k₂ [ES]                                        (rovnice iii).

Protože koncentrace volného enzymu [E] je

[E] = [Et] – [ES]                              (rovnice iv)

a podle následující rovnice (v) je

,

(kde K_d je disociační konstanta komplexu ES), platí pro ustálenou počáteční rychlost reakce

.

Srovnání této rovnice s rovnicí (ii) ukazuje, že:

• Konstanta k_kat = k₂, tj. k_kat je v tomto modelu rovno rychlostní konstantě 1. řádu charakterizující chemickou přeměnu komplexu ES po jeho vytvoření v prvním („fyzikálním“) stupni reakce;
• Konstanta K_M = k_-1 /k₁ = K_d, tj. K_M je v tomto modelu rovna skutečné rovnovážné disociační konstantě komplexu ES, a charakterizuje tak (podle (v)) pevnost vazby substrátu na enzym.

Mechanismus Briggse-Haldanea

Při ES ≡ EP, k_-2 ≡ k_-3 opět zanedbáváme, ale k₂ ≡ k₃ ≅ k-₁, jde o mechanismus, jehož rozbor podali G. E. Briggs a J. B. S. Haldane (1925). Opět platí (iii) a (iv), ale neplatí (v) – koncentrace [ES] nyní nebude rovnovážná. Koncentraci [ES] zde můžeme vypočítat z předpokladu stacionárnosti – jestliže je rychlost v po ustaveni stacionárního stavu stálá, je [ES] zřejmě také stálá.

Proto

a po výpočtu [ES] odtud a dosazení do (iii) je

Je patrné, že pro mechanismus Briggse-Haldanea zůstává k_kat = k₂ stejně, jako tomu bylo pro mechanismus Michaelise-Mentenové, ale K_M = (k_-1/k₁) + (k₂/k₁) > K_d, tj. K_M je nyní větší než skutečná rovnovážná disociační konstanta K_d komplexu ES; K_M je nyní nepravou, zdánlivou disociační konstantou komplexu ES. Při k₂ ≅ k_-1 je K_M ≅ 2K_d, a stacionární [ES] je tedy relativně menší než rovnovážná [ES]. Při k₂ ≪ k_-1 přechází zdánlivá K_M ve skutečnou rovnovážnou K_d (viz mechanismus Michaelise-Mentenové). Naopak při k₂ ≫ k_-1 je K_M ∼ k₂/k₁, tj. K_M ∼ k_kat/k₁ (viz níže mechanismus van Slyka a Cullena).

Mechanismus van Slyka a Cullena

Mechanismus, který je v jistém smyslu opakem mechanismu Michaelise-Mentenové a druhým krajním případem mechanismu Briggse-Haldanea, rozebrali D. D. van Slyke a G. E. Cullen (1914). Mechanismus předpokládá k₂ ≫ k_-1, a dovoluje tak zanedbat k_-1. V modelu (i) opět zůstává k₂ ≡ k₃, ES ≡ EP a k_-2 ≡ k_-3 zanedbáváme. Nahradíme-li nyní podle (v) a (vi) konstantu K_d jako míru afinity E k S konstantou K_M, platí

.

Podle (iii) potom je

v = k₁ [E] [S]                                     (rovnice vii)

Obdobnou rovnici získáme, jestliže v rovnici (ii) budeme uvažovat o velmi nízké koncentraci substrátu S - totiž že [S] ≪ K_M. Podle (iv) pak zároveň platí [E_t] ∼ [E], a tedy následující rovnice (viii):

.

Konstanta k₁ rovnice (vii) je konstantou prvního (fyzikálního) stupně reakce (i). Je konstantou 2. řádu. Neoznačujeme ji k_kat, protože k_kat rezervujeme pro reakce 1. řádu a vztahujeme ji k chemickým přeměnám v komplexu ES.

Ze srovnání rovnic (vii) a (viii) vyplývá, že veličina k_kat/K_M odpovídá k₁. Výraz k_kat/K_M lze interpretovat jako zdánlivou konstantu rychlosti 2. řádu charakterizující rychlost tvorby komplexu ES.

Pokud jde o  interpretaci K_M, ze (vii) a (viii) je zřejmé, že K_M ∼ k_kat/k₁.

Kompletní Haldaneův model

Jestliže konečně bereme v úvahu, že ES ≢ EP a počítáme se všemi konstantami modelu (i), potom, za předpokladu stacionárnosti, máme:

Odtud můžeme vypočítat /ES/ a /EP/:

Rychlost reakce je rovna rozdílu přímé a zpětné rychlosti některého stupně, např.

v = k₂[ES] – k_-2[EP]

V mezním případě, kdy [P] = 0, je

Odtud máme důležitou rovnici (ix)

a neméně důležitou rovnici (x)

.

Veličiny ^←k_kat a K_M^P pro reakci v obráceném směru by se vypočítaly obdobně.

Smysl konstanty k_kat

Z rovnice (ix) vyplývá, že v podrobnějších modelech lépe odpovídajících skutečnosti, jako je např. Haldaneův model, je konstanta k_kat kombinací různých rychlostních konstant 1. řádu a nemůže být přiřazena jednomu konkrétnímu stupni. Vyjma mezních případů, kdy může dosáhnout hodnoty některé ze skutečných konstant 1. řádu přímé reakce, je k_kat zdánlivou konstantou a je vždy menši než kterákoliv z konstant 1. řádu přímé reakoe. Představuje tedy dolní hranici rychlostních konstant chemických přeměn komplexu ES.

V literatuře je k_kat známa také pod označením „čislo přeměny“ anebo jako molekulová aktivita enzymu (tj. katalytická aktivita násobená počtem činných aktivnich míst na molekule enzymu).

Horní hranicí rychlostních konstant chemických mono- (neboli vnitřně-)molekulových přeměn je frekvence molekulových vibrací, tj. 10¹²-10¹³ s^-1.

Je-li nejpomalejšim stupněm n reakce rozpad komplexu EP, pak je k_kat rovna ryohlostní konstantě k_n tohoto stupně – v přikladu (i) by to mohla být konstanta k₃.

Smysl konstanty K_M

Z výrazu (x) vyplývá, že rovněž K_M^S (a popř. K_M^P) je kombinací různých konstant a nemůže být přiřazena určitému stupni. Může být větěí i menší než K_d anebo, v mezním případě, rovna K_d.

Jak ukazuje následující rovnice (xi), konstanta K_M^S je mírou celkového množství enzymu, které je v té či oné formě vázáno se substrátem:

(Ʃ[ES] je součet všech forem enzymu vázaných se substrátem při jeho přeměnách v produkt). K_M^S je zdánlivou disociační konstantou komplexu ES.

Skutečná, pravá „K_M^S je mezní hodnotou

,

kde Ʃ[E] je součet všech enzymových forem přítomných při [S] = 0 a Ʃ[ES] představuje součet všech enzymových forem vázanýoh se S, když [S] = ∾.

Poměr k_kat/K_M

Podíl obou zdánlivýoh konstant k_kat/K_M, le rovněž považovat za zdánlivou konstantu. Tento výraz představuje dolní hranici možné hodnoty rychlostní konstanty 2. řádu k₁, která určuje rychlost tvorby komplexu ES.

Jestliže je, v mezním případě, rychlost enzymové reakce limitována rychlostí tvorby komplexu ES (tj. všechny konstanty přímé reakce, vyjma k₁, jsou mnohem větší než k_-1), je podle (vii) a (viii) podíl k_kat/K_M skutečnou mikroskopickou konstantou totožnou s k₁.

Horní hranicí hodnot konstanty k_kat/K_M = k₁ je hodnota difúzní konstanty k_D v daném prostředí.

Zdánlivá ryohlostní konstanta 2. řádu k_kat/K_M uvádí podle (vii) a (viii) do vztahu rychlost reakce s koncentrací volného enzymu. Ze vztahu

[E] = [Et] – Ʃ[ES]                             (rovnice xii)

a vztahu (xi) vyplývá rovnice (xiii):

Při [S] ≪ K_M je [E] ∼ [E_t] a při [S] ≅ K_M je [E] ≅ 1/2[E_t]. Až při [S] ≫ K_M (tj. nasycení enzymu) bude [E] ∼ 0 a rychlost reakce bude podle vztahu (ii) úměrná k_kat, a ne k_kat/K_M.

Vztah mezi zdánlivými kinetickými konstantami a rovnovážnou konstantou reakce

V rovnováze je celková ryohlost reakce (i) rovna 0, a proto při nízkých [S] a [P] podle (viii) platí

.

Odtud vyplývá následující, tzv. Haldaneův vztah (xiv), podle kterého je

.

Výraz na pravé straně rovnice (xiv) je roven rovnovážné konstantě reakce, K_rovn. Haldaneův vztah je důležitý tím, že vyjadřuje rovnovážnou konstantu K_rovn katalyzované reakce pomocí k_kat (popř. V_max) a K_M. Ukazuje, že K_rovn není pouhou kombinací konstant k_kat přímého a zpětného směru, ani není jednoduchou kombinací K_M^S a K_M^P.

Jestliže je K_M^S ∼ K_M^P, bude platit K_rovn ∼ k_kat^→/^←k_kat. Jestliže se však K_M^S a K_M^P budou od sebe navzájem výrazně lišit, pak také k_kat^→ a ^←k_kat budou odlišné od hodnot vypočtených s použitím rovnovážné konstanty a pro vysvětlení tohoto rozdílu se musí vzít v úvahu hodnoty K_M^S a K_M^P, tedy vazba substrátu, popř. produktu, na enzym. V mezním případě, kdy

,

se vysvětlení přímo opírá o hodnoty K_d komplexů ES a EP.

Příklad. Podle své konstanty K_rovn je např. syntéza S-adenosylmethioninu téměř reverzibilní, a proto by k_kat^→ přímého směru reakce by měla být rovna ^←k_kat zpětné reakce. Pokud je ale katalyzována S-adenosyltransferázou, probíhá tato reakoe v přímém směru téměř 5.10⁵ krát rychleji než ve zpětném směru. K_M^P je tedy téměř 5.10⁵ krát menší než K_M^S.

Reakce katalyzovaná S-adenosyltransferázou tak je příkladem katalýzy tzv. „jednosměrným“ enzymem. Obdobné příklady lze nalézt v reakcích katalyzovaných transportními a svalovými ATPázami aj. Jsou dokladem, že vazebná energie ligandů (S a P) může být použita jednou pro vazebné účely (v uvedeném příkladu – v činnosti S-adenosyltransferázy – pro vazbu produktu P), a jindy pro snížení aktivační energie a urychleni reakce (v uvedeném přikladu jde o urychlení reakce v přímém směru).

Kompetice většího počtu substrátů o aktivní místo

Rovnice (xiv) popisuje zvláštní případ obecnější situace, kdy o aktivní místo enzymu soutěží více substrátů. Máme-li zjistit poměr rychlostí, v jakém budou enzymem zpracovávány dva nebo více substrátů, lze podle (viii) použít

a

.

Poměr rychlostí potom vyjadřuje následující rovnice (xv):

.

Vyplývá z ní, že o přednostním zpracováni substrátu enzymem rozhoduje podíl k_kat/K_M, a ne pouze podíl hodnot K_M nebo V_max. Znovu se potvrzuje, že specifičnost katalyzátoru zahrnuje jak vazebnou, tak i rychlostní komponentu katalýzy.

Reakce limitované difúzí

Konstanta k₁ vystupující v rovnici (vii) je složenou konstantou, která zahrnuje konstanty všech jednotlivých stupňů celého procesu vazby S na E a vytvoření ES. Zpravidla jde o vícestupňový proces. Hodnota konstanty k_kat/K_M je potom limitována hodnotou rychlostní konstanty nejpomalejšího stupně vazby (např. nutností desolvataoe, konformační změny a pod.) a nemůže ji překročit.

Pro teoretický rozbor lze vazebný děj považovat za jednostupňový a soustředit se pouze na omezující vliv difúze na rychlost enzymové reakce. Níže se tedy přepokládá, že všechny ostatní stupně vazby jsou mnohem rychlejší než difúze.

Z přístupu rozpracovaného M. Smoluchowským (1917) vyplývá, že konstanta difúze k_D, s níž jedna (sférická) částice difunduje ke druhé a setkává se s ní, je rovna

,

kde ζ je viskozita prostředí. Při rovnosti poloměrů obou částio r_a = r_b vychází hodnota k_D ve vodě při 25 °C asi 7.10⁹ mol^-1.l.s^-1.

Odtud lze dovodit, že maximální hodnota k_D, určující frekvenci setkání S s E, je o 1 – 4 řády menší, než je teoretická horní hranice pro konstanty k_kat chemických přeměn komplexu ES. Proto počet srážek může být limitujícím faktorem rychlosti chemických (katalyzovaných) reakcí. V takových případech se hovoří o reakcích limitovaných difúzí.

Chemické stupně přeměny substrátu v produkt mohou probíhat rychleji než difúze. Děje se tak zpravidla tehdy, když jsou katalyzovány vysoce vyvinutými enzymy.

Je-li typickou hranicí k₁ ∼ k_D asi 10⁹ mol^-1.l.s^-1, pak pro vysoce vyvinuté enzymy by podle (vii) a (viii) měla veličina K_M = k_kat/k₁ dosahovat hodnoty kolem 10^-9 k_kat. Jestliže [S] ≪ K_M, pak podle (viii) je

v = 10⁹ . [E] . [S] ≅ 10⁹ [E_t] . [S]               (rovnice xvi)

Uvedený výraz představuje difúzní limit maximální rychlosti tvorby produktu pro případy, že jediným faktorem, který určuje další rychlost reakce, je katalytická schopnost enzymu.

„Evolučně dokonalý“ enzym

Z rovnioe (viii) je patrné, že při konstantní koncentraci substrátu může dojít ke zvýšení rychlosti následujícími cestami:

• Zvýšením [E_t]. Při zachováni všech ostatních parametrů se následně zvyšuje hodnota volného [E] (v souladu s (xii)). Možnost, že by za fyziologických podmínek mohla [E_t] překročit číselnou hodnotu K_M substrátu, však není příliš pravděpodobná. Zvyšování [E_t] („extenzívní cesta“) ani není žádoucí, protože klade nároky na proteosyntetioký aparát a na energetické zabezpečení jeho činnosti.
• Při stálé hodnotě [E_t] lze hodnotu [E] zvýšit zvětšením K_M. Potom se [E] zvyšuje v souladu se vztahem (xiii).
• Vzrůst K_M však má za následek pokles hodnoty podílu k_kat/K_M, a tedy snížení rychlosti v. Je proto žádoucí, aby zvýšení K_M bylo zároveň provázeno současným zvýšením k_kat -  jinými slov aby část vazebné energie, ušetřená zvětšením K_M, byla využita ke snížení aktivační energie chemické přeměny.

V případě, že K_M ≈ (k_-1 + k_kat)/k₁, může K_M vzrůst diky zvětšení pouze k_-1 beze změny k_kat. Potom hodnota k_kat/K_M skutečně poklesne.

Jindy však, což je žádaný případ, může K_M vzrůst diky zvětšení k_-1 i k_kat. Jestliže přitom roste k_kat rychleji než k_-1, spěje systém k dosažení mechanismu van Slyka a Cullena.

K podobnému závěru vede rozbor podrobnějších modelů (např. (i) a vztahů (ix) a (x)) – jestliže K_M roste díky zvětšení rychlostních konstant uni-molekulárních stupňů především přímého směru reakce, roste k_kat/K_M i při zvětšováni K_M.

Zvětšení k_kat pak dovoluje udržet V_max i při poklesu [E_t] („intenzívní cesta„).

Princip maximalizace K_M při zachování k_kat/K_M

Enzymy se skutečně vyvíjejí k vyšším K_M při zachování k_kat/K_M. Hovoří se o principu maximalizaoe K_M při zachování k_kat/K_M. Tento princip protiřečí rozšířenému mylnému dojmu, že čím „lepší“ je enzym, tím pevněji váže substrát. Je však v souladu s poznáním úlohy vnitřní vazebné energie v enzymové katalýze.

Za „evolučně dokonalý“ se považuje enzym, který má K_M^S ≫ [S] a (k_kat/K_M) ∼ k₁ ≅ 10⁸-10⁹ mol^-1 . l . s^-1 ≈ k_D. Jak ukazuje rovnice xvi, zpracování substrátu takovým enzymem probíhá rychlostí difúze.

Hodnoty K_M, a k_kat/K_M nemohou růst nad všechny meze. Přesnější analýzy posunují hodnoty K_M do okolí K_M ∼ [S], k₂ do oblasti k₂ ∼ k_-1 a hodnoty k_kat/K_M k maximu asi pouze 10^-1 k1 anebo níže.

Kritéria bývají odvozována z předpokladu, že enzym má zajistit co největší reakční tok. Tento předpoklad není univerzální. Nezahrnuje např. enzymy, které zajišťují plynulý tok produktů i přes to, že hladiny jejich substrátů výrazně kolísají (např. proteolytické trávicí enzymy), anebo enzymy, které mají v metabolickýoh cestách regulační úlohu. Kromě toho se „katalytioká dokonalost“ izolovaného enzymu nemusí shodovat s dokonalostí enzymových komplexů, které jsou činné in vivo. Enzymy se vyvíjejí v rámci složitějších biokatalytických systémů a ani dosažení maximálnich hodnot kritéria k_kat/K_M při vysokých K_M nevyčerpává veškeré možnosti jejich evoluce.

Hodnota k_kat/K_M termodynamicky nevýhodné reakce nemůže, jak vyplývá ze vztahu (xiv), dosáhnout katalytického limitu – hodnota k_kat/K_M zpětné reakce by pak přesáhla difúzní limit.

Kinetický potenciál

Poměr k_kat/K_M se někdy také označuje jako katalytický potenciál anebo jako katalytický výkon, katalytická aktivita.

Pro výstižnější hodnocení skutečné katalytické schopnosti in situ se nahrazuje poměrem V_max/K_M (kinetický potenciál neboli kinetický výkon, kinetická aktivita). I tento poměr je zdánlivou konstantou 1. řádu. Ze vztahů (ii) a (iii) vyplývá, že je roven rychlosti přeměny jednotkové koncentrace substrátu v podmínkách, kdy [S] je faktorem limitujícím rychlost.

Teoretickou horní hranicí hodnot V_max/K_M je (analogicky ke kritériu k_kat/K_M) hodnota

V_max/K_M =  k₁[E_t]

při k₁ = k_D.

Zpracoval: Jaroslav Veselý, Ústav patologické fyziologie LF UP v Olomouci a Katedry fyziologie a patofyziologie LF OU v Ostravě.